8.3 การย่อ - ขยายภาพ (Scaling)
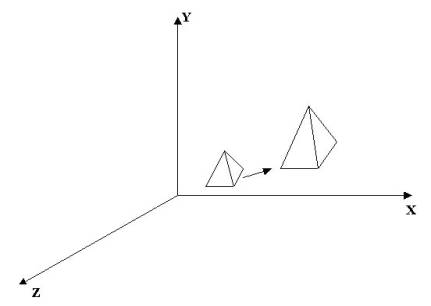
การย่อ - ขยายภาพในแบบ 3 มิติคิดเหมือนกับการย่อ - ขยายภาพในแบบ 2 มิติ
โดยคูณ scaling factor กับทุกจุดที่ใช้นิยามภาพ ดังนี้
X
= X * Sx
Y
= Y * Sy
Z
= Z * Sz
จากสมการ สามารถเขียนในรูปของ Matrix ได้ดังนี้
Sx 0 0 0
[
X Y Z 1] =
[ X Y Z 1] 0 Sy 0 0
0 0 Sz 0
0 0 0 1
ในทางปฏิบัติเราสามารถย่อ - ขยายภาพ ณ Fixed point ใด ๆ
ที่ไม่ใช่จุดกำเนิดซึ่งมีขั้นตอนในการทำ 3 ขั้นตอนดังนี้
1.
ย้าย Fixed
point ใดๆไปยังจุดกำเนิด (0,0,0)
2.
ทำการ ย่อ ขยายภาพ ที่จุดกำเนิด
3.
ย้าย Fixed
point กลับที่เดิม
ซึ่ง 3
ขั้นตอนสามารถนำ Transformation
Matrix ของแต่ละขั้นตอนมาคูณกันก่อนแล้วจึงนำไปคูณกับจุดแต่ละจุดที่ใช้นิยามภาพจะทำให้ง่ายขึ้น
1 0 0 0 Sx 0 0 0 1 0 0 0
[ X Y Z 1] =
[ X Y Z 1] 0 1 0 0 0 Sy 0 0 0 1 0 0
0 0 1 0 0 0 Sz 0 0 0 1 0
Tx Ty Tz 1 0 0 0 1 -Tx -Ty -Tz 1