4.4 การบิดภาพ ( Shearing)
การบิดภาพจะทำให้บางส่วนของภาพหรือภาพทั้งหมดเกิดการบิดเบือนขึ้น
ในที่นี้เราจะพิจารณาเพียง 2 แบบคือ การบิดภาพทางแกน X และการบิดภาพทางแกน
Y
การบิดภาพทางแกน Y จะทำให้เกิดการย้ายจุด (X,Y)
ไปยังจุด (X,Y) โดยที่
X
= X
Y
= Shy*X + Y ,Shy ¹ 0
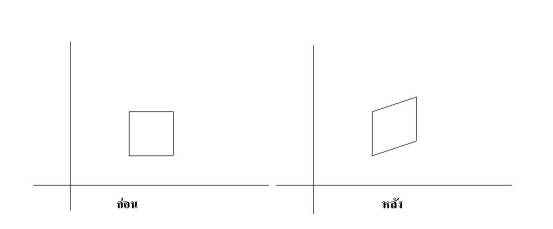
การบิดภาพทางแกน Y จะทำให้จุดต่าง ๆในแกน Y เลื่อนขึ้นหรือลงขึ้นอยู่กับเครื่องหมายของ Shy factor
จากสมการการบิดภาพดังกล่าว สามาเขียนในรูปแบบของ Matrix ได้ดังนี้
1 Shy 0
[
X Y 1] = [
X Y
1] 0 1 0
0 0 1
1 Shy 0
เรียก 0 1 0 ว่า Transformation Matrix สำหรับการบิดในแนวแกน Y
0 0 1
สำหรับการบิดภาพทางแกน X จะให้ผลตรงกันข้ามกับกากบิดภาพทางแกน
Y กล่าวคือจุด (X,Y) ของภาพจะถูกแปลงไปเป็นจุด
(X,Y) โดยที่
Y
= Y
X
= Shx*Y + X ,Shx ¹ 0
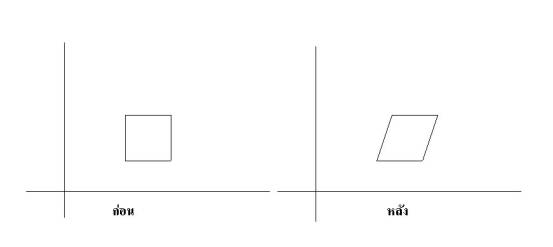
การบิดภาพทางแกน X จะทำให้จุดต่าง ๆในแกน X เลื่อนขึ้นหรือลงขึ้นอยู่กับเครื่องหมายของ Shx factor
จากสมการการบิดภาพดังกล่าว สามาเขียนในรูปแบบของ Matrix ได้ดังนี้
1 0 0
[
X Y 1] = [
X Y
1] Shx 1 0
0 0 1
1 0 0
เรียก Shx 1 0 ว่า Transformation Matrix สำหรับการบิดในแนวแกน X
0 0 1