4.3 การย่อ ขยายภาพ ( Scaling)
ภาพวัตถุสามารถเปลี่ยนขนาดได้โดยการเปลี่ยนระยะห่างระหว่างจุด นั่นคือ
การคูณจุดทุกจุดที่ใช้นิยามภาพกับระยะห่างระหว่างจุดซึ่งเป็นที่ค่าทำให้ระยะห่างมากขึ้นหรือทำให้ระยะห่างลดลง
ค่านี้เรียกว่า Scaling factor ถ้าค่า Scaling factor มากกว่า 1 ก็จะได้ภาพขยาย ถ้าค่านี้มีค่าน้อยกว่า 1 ก็จะได้เป็นภาพย่อ
ถ้าเท่ากับ1 ก็หมายถึงไม่มีผลต่อภาพวัตถุ
เมื่อใดก็ตามที่มีการย่อหรือขยายภาพ จะต้องมีจุด จุดหนึ่งซึ่งจะเรียกว่า fixed
point ของการย่อขยายภาพซึ่งใช้สำหรับเป็นจุดอ้างอิง
ถ้าให้จุดกำเนิด(0,0) เป็น fixed point จุด (X,Y) ใด ๆ ของภาพ ก็จะสามารถย่อหรือขยายได้โดยการคูณด้วย Sx factor สำหรับทิศทางในแกน X และ Sy factor สำหรับทิศทางในแกน Y ก็จะได้จุดใหม่ ( X,Y) ดังนี้
X
= X * Sx
Y
= Y * Sy
จากสมการการย่อ - ขยายภาพดังกล่าว สามาเขียนในรูปแบบของ Matrix ได้ดังนี้
Sx 0 0
[
X Y 1] = [
X Y
1] 0 Sy 0
0 0 1
Sx 0 0
เรียก 0 Sy 0 ว่า Transformation Matrix สำหรับการย่อ ขยาย
0 0 1
ถ้า Sx ไม่เท่ากับ Sy ผลก็คือภาพที่ได้จากการย่อหรือขยายจะเกิดการผิดเพี้ยนไปจากภาพเดิม
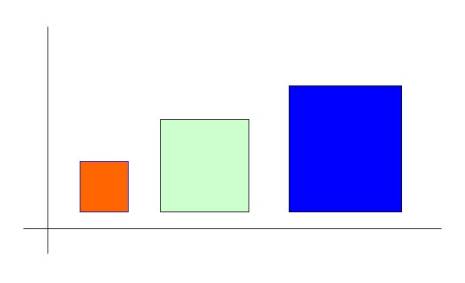
ถ้า Scaling factor มากกว่า 1 ภาพที่ถูกขยายแล้ว
จะถูกเคลื่อนย้ายห่างออกไปจาก fixed point ถ้า Scaling factor น้อยกว่า 1 ภาพที่ถูกย่อแล้ว
จุถูกเคลื่อนย้ายเข้ามาใกล้กับ fixed point มากขึ้น ดังรูป
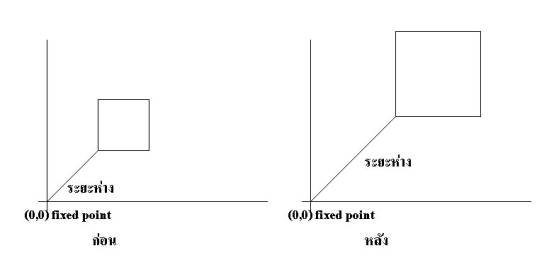
Fixed
point สำหรับการย่อหรือขยายภาพอาจจะไม่ใช่จุดกำเนิดก็ได้
ถ้าเป็นจุดใด ๆ จะต้องใช้ 3 ขั้นตอนดังนี้
1.
ย้าย Fixed point (Xf,Yf) ไปยังจุดกำเนิด (0,0)
โดยนำ Transformation Matrix
สำหรับการย้าย มาคูณกับจุดทุกจุดที่ใช้นิยามภาพ และให้ Tx = -Xf และ Ty
= -Yf เมื่อย้ายแล้ว
ทุกจุด(X,Y) ที่ใช้นิยามภาพก็จะถูกย้ายไปยังจุดใหม่ (X,Y) ด้วย
1 0 0
[
X Y 1] = [ X Y 1] 0 1 0
-Xf -Yf 1
2.
ทำการย่อหรือขยายภาพโดยที่ Fixed point อยู่ที่จุดกำเนิด(0,0)
เป็นระยะ Sx , Sy ทำได้โดยการนำ Transformation Matrix
สำหรับการย่อ - ขยายมาคูณกับจุดทุกจุดที่ได้จากข้อ 1
ได้จุดใหม่เป็น (X,Y)
Sx 0 0
[
X Y 1] = [
X Y
1] 0 Sy 0
0 0 1
3.
ย้าย Fixed point จากจุดกำเนิด(0,0)
กลับไปยังจุดเดิม (Xf,Yf)
จะได้จุดใหม่ของทุกจุดที่นิยามภาพเป็น (X*,Y*)
1 0 0
[
X* Y* 1] = [ X Y 1] 0 1 0
Xf Yf 1
จาก 3 ขั้นตอนข้างต้นเราอาจหาจุดใหม่โดยการประยุกต์ดังนี้ คือ นำ Transformation
Matrix มาคูณกันก่อน
1 0 0 Sx 0 0 1 0 0
0 1 0 0 Sy 0 0 1 0
-Xf -Yf 1 0 0 1 Xf Yf 1
Sx 0 0
= 0 Sy 0
(1-Sx)Xf (1-Sy)Yf 1
จากนั้นนำ Transformation Matrix ใหม่ที่ได้มาคูณกับจุดทุกจุดที่นิยามภาพ
Sx 0 0
[X Y 1] = [X Y 1]
0 Sy 0
(1-Sx)Xf (1-Sy)Yf 1
ก็จะได้ภาพที่ถูกย่อหรือขยายตามต้องการ ทั้งนี้ต้องคูณ Transformation
Matrix ตามลำดับขั้นตอนของการ Transform เนื่องจากถ้าคูณผิดลำดับหรือสลับกันแล้วภาพที่ได้ก็จะผิดไปจากความเป็นจริง