4.2การหมุนภาพ ( Rotation)
การหมุนภาพเป็นการแปลงรูปที่จะต้องกำหนดว่าจุดใดจุดหนึ่งเป็นจุดหมุน
(pivot
point) เสมอ หลังจากหมุนภาพไปแล้ว
ระยะห่างระหว่างจุดหมุนกับภาพจะยังคงมีค่าเท่าเดิม รูปร่าง
ลักษณะของภาพก็ยังคงเดิม แต่ภาพจะมีการจัดวางที่ต่างไปจากเดิม
เนื่องมาจากการหมุนนั่นเอง
การหมุนภาพอาจจะหมุนทีละหลาย ๆภาพก็ได้
จะหมุนทวนเข็มนาฬิกา(ค่ามุมเป็นบวก) หรือ หมุนตามเข็มนาฬิกาก็ได้(ค่ามุมเป็นลบ)
และจุดหมุนที่ใช้อาจจะอยู่ภายในภาพหรือภายนอกภาพก็ได้
การอ้างถึงจุดพิกัด (X,Y) นั้น นอกจากจะใช้ระบบพิกัดฉากแล้ว
อาจจะใช้ระบบพิกัด Polar (การบอกตำแหน่งจุดโดยใช้ Vector
) ก็ได้ ซึ่งทั้งสองระบบมีความสัมพันธ์กันดังนี้
X
= rcosf
Y
= rsinf
ถ้า(X,Y) ถูกหมุนไปจากเดิมเป็นมุม q
ในทิศทางทวนเข็มนาฬิกาจะได้จุดใหม่คือ (X,Y) ดังรูป
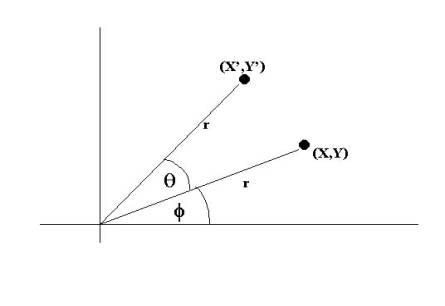
จะได้
X
= rcos(f+q) = rcosfcosq - rsinfsinq
Y
= rsin(f+q) = rsinfcosq + rcosfsinq
แทนค่า rcosf ด้วย X
และ rsinf ด้วย Y
จะได้
X
= Xcosq - Ysinq
Y
= Ycosq + Xsinq
สมการที่ได้นี้คือ สมการที่ใช้แปลงค่าพิกัดจากจุด (X,Y) ไปเป็นจุดใหม่ (X,Y) โดยการหมุนรอบจุดกำเนิดไปเป็นมุม
q ทิศทางทวนเข็มนาฬิกา
การหมุนภาพทำได้โดยการแปลงค่าพิกัดจุดทุกจุดที่ใช้นิยามภาพนั้นไปเป็นพิกัดใหม่โดยใช้สมการข้างต้นแล้วค่อยวาดภาพเดิมที่จุดพิกัดใหม่นั้น
จากสมการการหมุนภาพดังกล่าว สามาเขียนในรูปแบบของ Matrix ได้ดังนี้
![]()
![]() cosq sinq 0
cosq sinq 0
[
X Y 1] = [
X Y
1] -sinq cosq 0
0 0 1
![]()
![]() cosq sinq 0
cosq sinq 0
เรียก -sinq cosq 0 ว่า Transformation Matrix สำหรับการหมุน
0 0 1
ในทางปฏิบัติเราอาจจะต้องหมุนภาพรอบจุดใด ๆ ซึ่งไม่ใช่จุดกำเนิด
สำหรับกรณีนี้จะต้องใช้ 3 ขั้นตอน ดังนี้
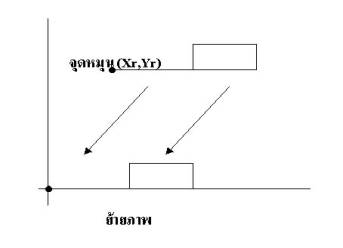
1.
ย้ายจุดหมุน (Xr,Yr)ไปยังจุดกำเนิด (0,0)
โดยนำ Transformation Matrix สำหรับการย้ายมาคูณกับจุดทุกจุด
และให้ Tx = -Xr และ Ty = -Yr เมื่อย้ายแล้ว ทุกจุด(X,Y) ที่ใช้นิยามภาพก็จะถูกย้ายไปยังจุดใหม่ (X,Y)
ด้วย
![]()
![]() 1 0 0
1 0 0
[
X Y 1] = [ X Y 1] 0 1 0
-Xr -Yr 1
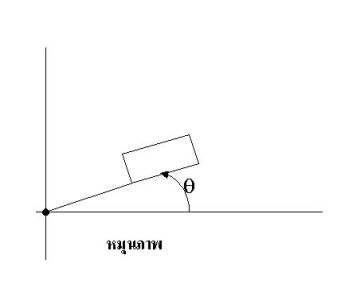
2.
ทำการหมุนภาพรอบจุดกำเนิด(0,0) เป็นมุม q ทำได้โดยการนำ Transformation Matrix สำหรับการหมุนมาคูณกับจุดทุกจุดที่ได้จากข้อ 1 ได้จุดใหม่เป็น (X,Y)
![]()
![]() cosq sinq 0
cosq sinq 0
[
X Y 1] = [
X Y
1] -sinq cosq 0
0 0 1
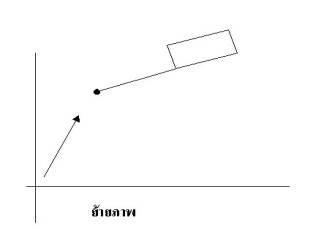
3.
ย้ายจุดหมุนจากจุดกำเนิด(0,0) กลับไปยังจุดเดิม (Xr,Yr)
จะได้จุดใหม่ของทุกจุดที่นิยามภาพเป็น (X*,Y*)
![]()
![]() 1 0 0
1 0 0
[
X* Y* 1] = [ X Y 1] 0 1 0
Xr Yr 1
จาก 3 ขั้นตอนข้างต้นเราอาจหาจุดใหม่โดยการประยุกต์ดังนี้ คือ นำ Transformation
Matrix มาคูณกันก่อน
![]()
![]()
![]()
![]()
![]()
![]() 1 0 0 cosq sinq 0 1 0 0
1 0 0 cosq sinq 0 1 0 0
0 1 0 -sinq cosq 0 0 1 0
-Xr -Yr 1 0 0 1 Xr Yr 1
![]() cosq sinq 0
cosq sinq 0
![]() = -sinq cosq 0
= -sinq cosq 0
(1-
cosq)Xr + Yrsinq (1-cosq)Yr - Xrsinq 1
จากนั้นนำ Transformation Matrix ใหม่ที่ได้มาคูณกับจุดทุกจุดที่นิยามภาพ
![]()
![]()
cosq sinq 0
[X Y 1] = [X Y 1]
-sinq cosq 0
(1-
cosq)Xr + Yrsinq (1-cosq)Yr - Xrsinq 1
ก็จะได้ภาพที่ถูกหมุนตามต้องการ ทั้งนี้ต้องคูณ Transformation
Matrix ตามลำดับขั้นตอนของการ Transform เนื่องจากถ้าคูณผิดลำดับหรือสลับกันแล้วภาพที่ได้ก็จะผิดไปจากความเป็นจริง