บทที่ 6 เส้นโค้ง(Curve)

ในการลากเส้นนั้นเรามีวิธีการลากเส้นอยู่ 2 แบบ คือ

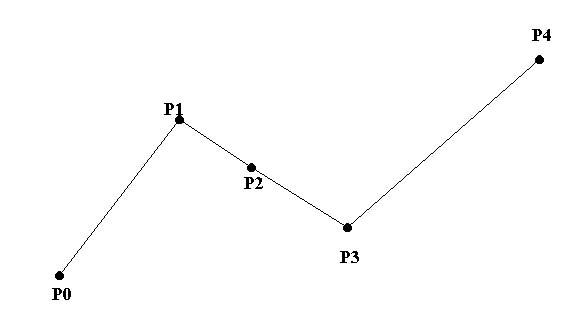
1. Interpolation เป็นการลากเส้นแบบลากเส้นตรงเชื่อมจุดทุกจุดดังรูป

2. Approximation เป็นการประมาณค่าจุดต่อไปโดยใช้จุดรอบ ๆข้าง ดังรูป

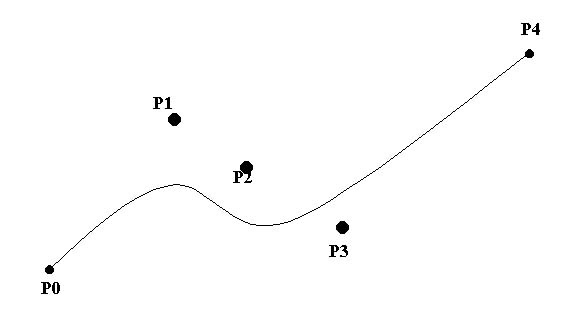
ซึ่ง Approximation จะนำไปสู่การวาดเส้นโค้ง

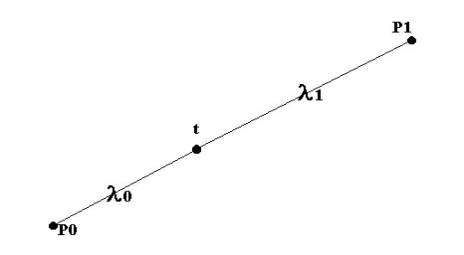
l0*P0 + l1*P1 = P (1)

l0 = 1 - l1 (2)

ถ้า l1 = t (3)

แทนค่า (2) ใน (1) (1 - l1)*P0 + l1*P1 = P (4)

แทนค่า (3) ใน (4) (1 – t )*P0 + t*P1 = P

ดังนั้น P(x,y) = (1 - t)*P0 + t*P1

จากวิธีการดังกล่าวได้มีการนำมาประยุกต์เป็น Algorithm สำหรับการลากเส้นโค้งโดยในที่นี้เราจะกล่าวถึงเพียง Algorithm เดียว คือ Bezier Curve Algorithm

Curve 3 Control point

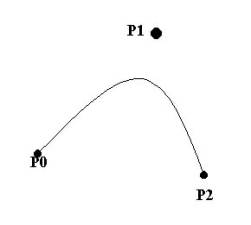
P(x,y) = (1 - u)*P0 + 2*u*(1-u)*P1 + u²*P2

Curve 4 Control point

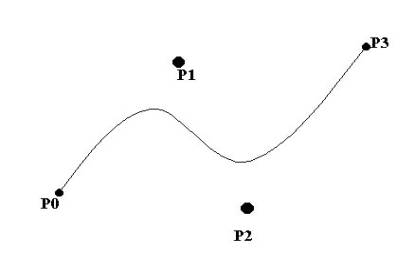
P(x,y) = (1 - u)³*P0 + 3*u*(1-u)²*P1 + 3*u²*(1 - u)*P2 + u³*P3

Curve n + 1 Control point

_n

P(u) = S B_k,n(u) P_k

^{k = 0}

Bk,n(u) = C(n,k) u^k ( 1 - u )^n-k

C(n,k) = n! / (k! ( n - k )!)

โดย u คือ ระยะห่างของจุดที่ต้องการจะ plot ภายใน control point

Bezier Curve Algorithm 3 control point

Void Bezier(int cpx, int cpy, int N, int *x, int *y)

{

Du = 1/N;

u = 0 ;

for(int I = 1; I < = N ; I++)

{

w = 1- u;

B0z = w*w;

B1z = 2*u*w;

B2z = u*u;

x[I] = (B0z*cpx[1]) + (B1z*cpx[2]) + (B2z*cpx[3]);

y[I] = (B0z*cpy[1]) + (B1z*cpy[2]) + (B2z*cpy[3]);

u = u + Du;

}

}

Back Next