3.2 วงกลม(Circle)

3.2.1 วงกลมตามทฤษฎีเชิงมุม

สมการวงกลมสามารถเขียนในรูปสมการเชิงมุมได้ดังนี้

X =Xc + r* cosq

Y =Yc + r* sinq

โดยที่ q มีค่าอยู่ระหว่าง 0 ถึง 2p เนื่องจาก ความยาวของส่วนโค้งมีค่าเท่ากับ r * q (มาจากสูตรเส้นรอบวงวกลม =2pr) และ r เป็นรัศมีของวงกลมมีค่าคงที่ ดังนั้น ส่วนโค้งของวงกลมจึงขึ้นกับ q จุดพิกัดที่จะ plot เพื่อลากเส้นต่อกันเป็นส่วนโค้งของวงกลม จึงขึ้นกับ q ด้วยเมื่อเราเปลี่ยนค่าของ q จาก0 ถึง 2p โดยเปลี่ยนไปทีละ dq แล้ว plot จุดพิกัดที่สอดคล้องกันก็จะได้วงกลมตามต้องการ

จากสมการเชิงมุมดังกล่าวเราสามารถนำมาเขียนเป็น Algorithm ได้ดังนี้

1. Input รัศมี(r) ,จุดศูนย์กลางวงกลม(Xc,Yc) และ จำนวนจุดที่ต้องการจะplot(n)

2. คำนวณหา dq = 44/ (7*n)

3. plot (r +Xc,0+Yc) เป็นจุดแรก

4. คำนวณหาจุดที่จะ plot ต่อไป ดังนี้

X_k+1 = Xc + r*cos(q)

Y_k+1 = Yc + r*sin(q)

q_k+1 = q_k + dq

5. plotจุด (X_{k + 1},Y_{k + 1})

6. ทำซ้ำ ข้อ 4,5 เป็นจำนวน n ครั้ง

3.2.2 Midpoint Circle Algorithm

1. Input รัศมี(r) ,จุดศูนย์กลางวงกลม(Xc,Yc) โดยจุดแรกที่จะ plot บนเส้นรอบวง ของ วงกลมที่มีศูนย์กลางอยู่ที่จุดกำเนิด คือ(X0,Y0) = (0,r)

2. คำนวณค่าเริ่มต้นสำหรับการตัดสินใจในการคำนวณหาจุดที่จะ plot ต่อไป ดังนี้ P₀ = 5/4 – r (float) หรือ P0 = 1- r (Integer)

3. ที่แต่ละตำแหน่ง X_k เริ่มที่ k = 0

IF P_k < 0 then

จุดต่อไปบนเส้นรอบวงสำหรับวงกลมที่มีจุดศูนย์กลางที่ (0,0) คือ (X_k + 1,Y_k) และ P_k+1 = P_k +2X_k+1

Else

จุดต่อไป คือ (X_k + 1,Y_k - 1) และ P_k+1 = P_k +2X_k+1 + 1 – 2Y_k+1

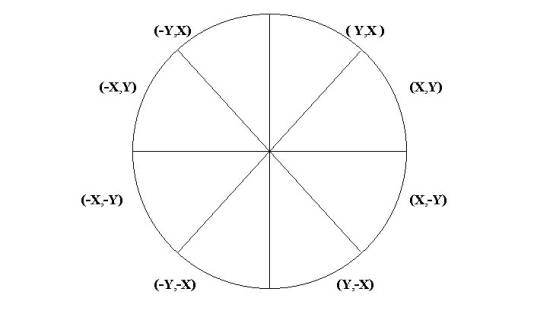
4. กำหนดจุดที่สมมาตรใน 7 ส่วนที่เหลือ

5. บวกจุดศูนย์กลางวงกลมกับจุดที่คำนวณได้แต่ละจุด ดังนี้

X = X + Xc

Y = Y +Yc

จากนั้นจึงทำการplotจุด (X,Y)

6. ทำซ้ำ ข้อ 3,4,5 จนกระทั่ง X>=Y

สมมาตรของวงกลมทั้ง 8 ส่วนแสดงได้ดังนี้

Back Next